Persamaan Kuadrat Kelas 9
Pengertian Persamaan Kuadrat
Persamaan kuadrat adalah persamaan yang variabelnya memiliki pangkat tertinggi sama dengan dua (2). Adapun bentuk umum persamaan kuadrat adalah sebagai berikut.
ax2 + bx + c = 0
Keterangan:
a, b = koefisien (a ≠ 0);
x = variabel; dan
c = konstanta.
Jenis-Jenis Persamaan Kuadrat
Secara umum, persamaan kuadrat dibagi menjadi empat, yaitu sebagai berikut.
1. Persamaan Kuadrat Biasa
Persamaan kuadrat biasa adalah persamaan kuadrat yang nilai a = 1. Berikut ini contohnya.
x2 + 3x + 2 = 0
2. Persamaan Kuadrat Murni
Persamaan kuadrat murni adalah persamaan kuadrat yang nilai b = 0. Berikut ini contohnya.
x2 + 2 = 0
3. Persamaan Kuadrat Tak Lengkap
Persamaan kuadrat tak lengkap adalah persamaan kuadrat yang nilai c = 0. Berikut ini contohnya.
x2 + 3x = 0
4. Persamaan Kuadrat Rasional
Persamaan kuadrat rasional adalah persamaan kuadrat yang nilai koefisien dan konstantanya berupa bilangan rasional. Berikut ini contohnya.
4x2 + 3x + 2 = 0
Cara Menentukan Akar Persamaan Kuadrat
Akar persamaan kuadrat merupakan salah satu faktor penting yang harus bisa kamu tentukan dalam penyelesaian persamaan kuadrat. Ada beberapa cara yang bisa kamu gunakan untuk mencari akar pada persamaan kuadrat, yaitu sebagai berikut.
1. Faktorisasi
Faktorisasi adalah penjumlahan suku aljabar menjadi bentuk perkalian faktornya. Jika kamu melakukan faktorisasi persamaan kuadrat, artinya kamu membuat perkalian dua buah persamaan linear.
ax2 + bx + c = 0
b = hasil penjumlahan antara suku ke-1 dan ke-2
c = hasil perkalian antara suku ke-1 dan ke-2
Perhatikan contoh berikut.
- Bentuk persamaan kuadrat: x2 + 5x + 6 = 0
Bentuk faktorisasi: (x + 3) (x + 2) = 0
Akar: x = -3 atau x = -2
- Bentuk persamaan kuadrat: x2 – 9 = 0
Bentuk faktorisasi: (x – 3)(x + 3) = 0
Akar: x = 3 atau x = -3
2. Melengkapkan Kuadrat Sempurna
Bentuk ax2 + bx + c = 0 bisa kamu jabarkan menjadi seperti berikut.
(x + p)2 = q
Perhatikan contoh berikut.
Bentuk persamaan kuadrat: x2 + 5x + 6 = 0
x2 + 8x + 6 = 0
(x2 + 8x) = -6
x2 + 8x +16 = -6 +16
(x + 4)2 = 10
(x + 4) = ± √10
x = √10 – 4 atau x = -√10 – 4
3. Menggunakan Rumus abc
Adapun persamaan rumus abc adalah sebagai berikut.
Perhatikan contoh berikut.
Tentukan akar persamaan x2 – 4x – 5 = 0!
Diketahui: a = 1, b = -4, dan c = -5
Substitusikan nilai a, b, dan c ke persamaan abc.
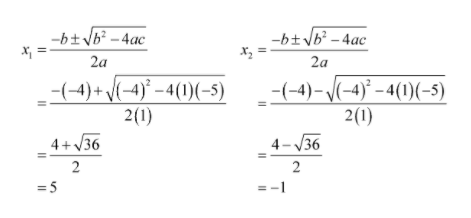
Jadi, akar persamaan x2 – 4x – 5 = 0 adalah x = 5 atau x = -1.
Jenis-Jenis Akar Persamaan Kuadrat
Sebelum membahas tentang jenis akar persamaan kuadrat, kamu akan dikenalkan terlebih dahulu dengan istilah diskriminan. Apa itu diskriminan? Diskriminan atau biasa dilambangkan D adalah hubungan antarkoefisien yang menentukan besar dan jenis akar persamaan kuadrat. Pada pembahasan sebelumnya, kamu sudah mengenal rumus abc, yaitu sebagai berikut.

Dari persamaan di atas, besaran yang dimaksud diskriminan adalah b2 – 4ac.
Dengan demikian, persamaan rumus abc menjadi seperti berikut.
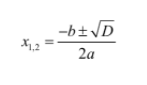
Nah, jenis akar persamaan kuadrat ternyata bergantung pada nilai dari determinannya (D). Berikut ini penjelasannya.
- Jika nilai D > 0, maka suatu persamaan kuadrat akan memiliki dua akar real yang tidak sama besar (x1 ≠ x2).
- Jika nilai D = 0, maka suatu persamaan kuadrat akan memiliki dua akar real dan kembar.
- Jika nilai D < 0, maka suatu persamaan kuadrat tidak memiliki akar real (akarnya imajiner).
Jika persamaan kuadrat ditulis dalam bentuk grafik, akan muncul grafik parabola seperti bentuk lintasan bola yang ditendang dengan kemiringan tertentu.





Komentar
Posting Komentar